David Williams
EF4
I was just wondering why higher lapse rate values are referred to as "steep"? I have a couple pet theories, but I never really seen that explained anywhere. Does anyone know?
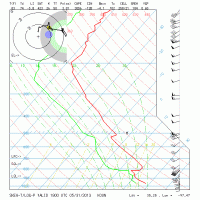
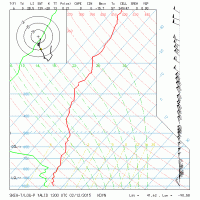
Yes, I see that if you represent it on a graph it would appear steeper. I was thinking about it as it appears on the Skew-T. Strange because we always look at the Skew-T to visualize the environmental lapse rates. On Skew-Ts "steep" lapse rates actually appear to have a more shallow slope than below normal (6.5 C/km) lapse rates.
Precisely my point! The entire reason we call it a Skew-T is because the temperature line is skewed. Therefore, why refer to the temperature line as being "steep" on a line that we all know has been purposefully augmented so that high values of lapse rates appear as a shallower line? Seems ironic or at least counter-intuitive.There's a reason such a plot is called a skew-T/log-P chart.
Precisely my point! The entire reason we call it a Skew-T is because the temperature line is skewed. Therefore, why refer to the temperature line as being "steep" on a line that we all know has been purposefully augmented so that high values of lapse rates appear as a shallower line? Seems ironic or at least counter-intuitive.
Very unscientific explanation: lapse rates are the rate in which temperature decreases going up in height. Thus the higher values are a faster rate of decrease. So if you represented that with a graph, your line would thus have a "steeper" curve as you increased your value. Hopefully that makes some sense.
Thank you Jeff! [emoji2]I think you're hung up on the idea that only a skew-T diagram can be used to assess stability.
This is the best response so far in this thread. You use the phrase "steep lapse rate". Lapse rate is defined as -dT/dz, or the rate of decrease of temperature with ascent. dT/dz is a mathematical symbol in calculus representing a "derivative", which is the instantaneous rate of change of a curve along some dimension (in this case, temperature along the dimension of vertical space). dT/dz also represents a slope when a finite distance is used. So when someone computes the lapse rate between 700 mb and 500 mb (typically referred to as mid-level lapse rates), which is a finite distance btw, then the result is the slope of the line connecting the temperature at 700 mb to the temperature at 500 mb. Large slopes are typically referred to as "steep", whereas low slope values can be referred to as "shallow". Think of it like driving through the Rockies on a highway. At some points you'll be ascending or descending mountains and there will be a sign to warn you of a steep grade approaching (e.g., "6% GRADE - NEXT 2 MILES"). If you saw a sign saying "1% GRADE - NEXT 12 MILES" you probably wouldn't think of that as a very steep slope because your elevation won't be changing much with horizontal distance compared to on the 6% grade (even though, in this case, your total elevation change at the end of the grade would be the same in both cases). Lapse rate works the exact same way.
What blurs the issue for me is that when the SPC talks about lapse rates... I think... they are always talking about ambient obs. So if that's true (is it???) then it makes no sense to call them steep on a day with big instability, unless it's not a reference to how it all LOOKS on a SkewT.
When the term "lapse rate" is used in any operational sense, what's being discussed is technically referred to as "environmental lapse rate", which is the lapse rate of the actual environment. "Steep" lapse rates refer exclusively to environmental lapse rates.
Parcel lapse rates are left for the classroom or scientific papers. Besides, there are only two values of a parcel lapse rate - dry and moist adiabatic.
the "steep" in "steep environmental lapse rates" must not have anything to do with Skew-T's
Which is why I was grateful that you explained the situation. your explanation purposefully left out sket-ts.This. This is one of the top 3 statements in this thread.
