Many regular chasers are probably familiar with the "veer-back" (or veer-back-veer; VBV) feature of forecast and observed hodographs and their relationship with disappointing storm chases. Most have noted in their own adventures that when backing is present aloft, storm mode becomes messy and the day usually ends up with little in the way of impressive structure or tornadoes. Since there is no formal thread on this forum (that I could find) on the academic background on the "veer-back" (hereafter, VB), I figured I would present this informative module on the subject.
Definition of veer-back(-veer)
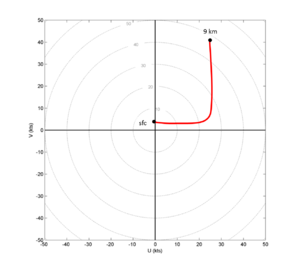
VBV refers to a backing of the winds in a layer above another layer with veering winds, and sometimes bounded above by another layer with veering winds (hence the second -veer in the name). The image below illustrates this feature:
I personally choose not to use the second "-veer" when describing this phenomenon since it seems to have little importance in the overall issue and is not always present. But to each his/her own.
For practice, the un-annotated image is linked below:
Before continuing on, I want to point out that what many refer to as VB is really a specific example of a more general phenomenon. What is really happening is a reversal of the curvature of the hodograph. While it is common for veering winds to be associated with clockwise/cyclonic hodograph curvature and backing winds with counter-clockwise/anticyclonic hodograph curvature, such a relationship is not required. The idealized example below shows a hodograph where the curvature switches from cyclonic to anticyclonic at an inflection point, z_i, even though the actual winds continue to veer through the inflection point itself.
(Note: at this point, if you are lost in the terminology or don't get it, I recommend a basic primer on hodographs, which I have not included here.)
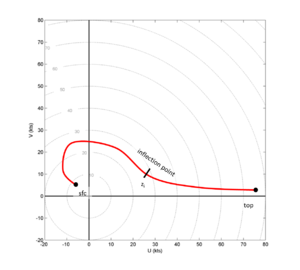
In the idealized hodograph above, there is cyclonic curvature from the surface to z_i and anticyclonic curvature above that. While still idealized, this is still a representative example of many hodographs seen in the US during the spring season. To drive the point home, I've included a very generalized example of this which is generally not representative of what you see in real life, but which exemplifies the true characteristics of this phenomenon:
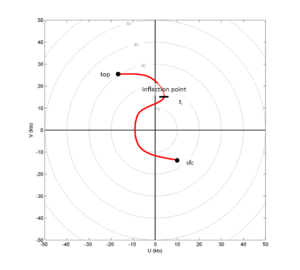
The characteristic shape of this hodograph lends itself to another name commonly used to describe it: the 'S-shaped hodograph'. When the "kink" or inflection point is more obvious, the association between veering and cyclonic curvature/backing anticyclonic curvature strengthens and becomes more evident.
Okay, so what's so important about VB?
The fundamental atmospheric quality that distinguishes supercells from non-supercell storm modes is vertical wind shear, which is best depicted by examining hodographs. Vertical wind shear is represented by the length of the hodograph, specifically, the distance in U-/V-wind parameter space (the axes of the hodograph) between two vertical levels. Typically the surface and 6-km AGL levels are used to define "deep layer" wind shear used to discriminate between supercell storm modes and non-supercell storm modes. Since the magnitude of shear is rather important (perhaps of first-order importance), supercell storms can still occur even with S-shaped hodographs. However, hodograph curvature tends to indicate which type of deviant motion is preferred. Cyclonically curved hodographs favor right-moving supercells. The reason for this has to do with how the shear vector interacts with the updraft of a storm and also on storm-relative helicity (it will be assumed that everyone knows what that is and how to analyze it). So when you have a combination of cyclonic and anticyclonic curvature, SRH is reduced for two reasons: 1) the inclusion of the area bounded by anticyclonic curvature; 2) the storm motion vector is closer to the hodograph itself, which reduces storm relative flow. Reduced SRH leads to less propensity for sustained updraft rotation, even in the presence of sufficient deep layer shear, and increased storm relative flow is pretty much always better than the alternative. Boring stuff happens when storm relative flow is small.
In summary, with S-shaped hodographs storm modes tend to get messy, even if the forcing supports cellular convection.
VB and tornado potential
Just the presence of VB/S-shape in a hodograph does not automatically preclude tornado potential. Tornadoes depend much more strongly on low level shear than deep layer shear, and many S-shaped hodographs still contain sufficient low level shear for tornadoes. So why are tornadoes still less common in environments with S-shaped hodographs? Tornadoes cannot just form out of nothing. They need a supportive/nurturing environment, which includes sufficient buoyancy to accompany that shear, and basically an absence of something else to screw all of that up. Downdrafts, outflow, and cold pools can be excellent tornado disruptors, especially since they are sources of negative buoyancy and downward accelerations (both of which are toxic to tornado production). Since environments with S-shaped hodographs tend to favor messy storms, it's usually the behavior of the parent thunderstorm that restricts or eliminates the favorable environment for a tornado to form. Tornadoes can still form if the environment doesn't get too messed up, but it is simply more common for disruption to occur with these hodographs.
My hypothesis about how impactful S-shaped hodographs can be on supercells
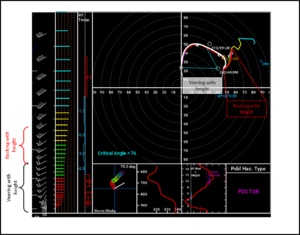
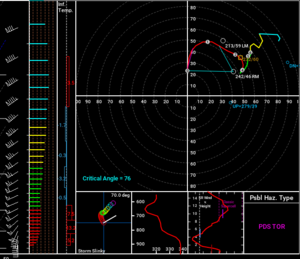
In the 2016 Severe Local Storms Conference, Matt Parker presented some research on the impact of VB on supercells (https://ams.confex.com/ams/28SLS/webprogram/Paper300986.html). A cursory examination of his results surprised me, as he tested several hodographs that featured either VB, a kink, or some sort of S-shape (all examples of the reversal of hodograph curvature). This led to a broad conclusion that VB really doesn't matter when it comes to supercell behavior. This result seems at odds with my own personal observations, and I think many other chasers would agree that storms seem to struggle to get or stay organized in environments with S-shaped hodographs. The research Matt did looks legitimate, so I had to follow along more closely to see where the discrepancy arises. My hypothesis is that the height of the inflection point (where the hodograph curvature reverses) is critical in determining whether supercells will thrive in an S-shaped hodograph environment. Specifically, when the inflection point is higher, it is more likely that supercells will thrive. A general threshold seems to be about 3 km AGL. In the 9 hodographs he tested (below; shamelessly ripped from his recorded presentation), the inflection point is below 3 km in only one hodograph - "the fish hook" - and that is the only case in which a sustained supercell does not appear:
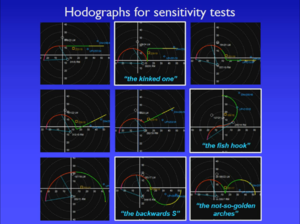
This is a bit subtle, but here is the explanation. If you're familiar with SHARPPY, then you know the hodograph color changes from red to green at the 3 km AGL mark. In the 7 hodographs above that have an inflection point, in only "the fish hook" hodograph does the inflection point occur in the red section. Even though it appears visually slight, it is there. And the results show that a storm struggled to survive in that environment. Surprisingly, he did not discuss the 0-3 km SRH values in these hodographs except for "the fish hook" which had 69 m2/s2 0-3 km SRH, a puny value if you want supercells. 0-3 km shear (not SRH) has been shown in some recent research to be a potentially skillful discriminator between weak and strong tornadoes, and it's not much of a stretch to consider the discriminatory nature of 0-3 km SRH to supercell and tornado production in general. Matt did mention at the end of his talk that it would be worth testing the sensitivity of these simulations to the height of the inflection point, but to my knowledge this research has yet to be conducted. I suspect whoever does it will find decreasing sustainability/organization in storms as the height of the curvature reversal decreases.
TL;DR
When assessing the impact of VB(V) on storm organization, the height at which the backing begins is probably pretty important, with increased potential for sustained supercells with increasing height. So don't despair just because you see VB in a sounding. You can still get relatively clean supercells and tornadoes with S-shaped hodographs. In fact, there was a little nugget towards the end of Matt's presentation suggesting that above a certain height, some degree of backing can actually be beneficial in that it can restrict left movers/splits, thus keeping the environment relatively undisturbed and allowing storms to rage for much longer.
Definition of veer-back(-veer)
VBV refers to a backing of the winds in a layer above another layer with veering winds, and sometimes bounded above by another layer with veering winds (hence the second -veer in the name). The image below illustrates this feature:

I personally choose not to use the second "-veer" when describing this phenomenon since it seems to have little importance in the overall issue and is not always present. But to each his/her own.
For practice, the un-annotated image is linked below:

Before continuing on, I want to point out that what many refer to as VB is really a specific example of a more general phenomenon. What is really happening is a reversal of the curvature of the hodograph. While it is common for veering winds to be associated with clockwise/cyclonic hodograph curvature and backing winds with counter-clockwise/anticyclonic hodograph curvature, such a relationship is not required. The idealized example below shows a hodograph where the curvature switches from cyclonic to anticyclonic at an inflection point, z_i, even though the actual winds continue to veer through the inflection point itself.
(Note: at this point, if you are lost in the terminology or don't get it, I recommend a basic primer on hodographs, which I have not included here.)

In the idealized hodograph above, there is cyclonic curvature from the surface to z_i and anticyclonic curvature above that. While still idealized, this is still a representative example of many hodographs seen in the US during the spring season. To drive the point home, I've included a very generalized example of this which is generally not representative of what you see in real life, but which exemplifies the true characteristics of this phenomenon:

The characteristic shape of this hodograph lends itself to another name commonly used to describe it: the 'S-shaped hodograph'. When the "kink" or inflection point is more obvious, the association between veering and cyclonic curvature/backing anticyclonic curvature strengthens and becomes more evident.
Okay, so what's so important about VB?
The fundamental atmospheric quality that distinguishes supercells from non-supercell storm modes is vertical wind shear, which is best depicted by examining hodographs. Vertical wind shear is represented by the length of the hodograph, specifically, the distance in U-/V-wind parameter space (the axes of the hodograph) between two vertical levels. Typically the surface and 6-km AGL levels are used to define "deep layer" wind shear used to discriminate between supercell storm modes and non-supercell storm modes. Since the magnitude of shear is rather important (perhaps of first-order importance), supercell storms can still occur even with S-shaped hodographs. However, hodograph curvature tends to indicate which type of deviant motion is preferred. Cyclonically curved hodographs favor right-moving supercells. The reason for this has to do with how the shear vector interacts with the updraft of a storm and also on storm-relative helicity (it will be assumed that everyone knows what that is and how to analyze it). So when you have a combination of cyclonic and anticyclonic curvature, SRH is reduced for two reasons: 1) the inclusion of the area bounded by anticyclonic curvature; 2) the storm motion vector is closer to the hodograph itself, which reduces storm relative flow. Reduced SRH leads to less propensity for sustained updraft rotation, even in the presence of sufficient deep layer shear, and increased storm relative flow is pretty much always better than the alternative. Boring stuff happens when storm relative flow is small.
In summary, with S-shaped hodographs storm modes tend to get messy, even if the forcing supports cellular convection.
VB and tornado potential
Just the presence of VB/S-shape in a hodograph does not automatically preclude tornado potential. Tornadoes depend much more strongly on low level shear than deep layer shear, and many S-shaped hodographs still contain sufficient low level shear for tornadoes. So why are tornadoes still less common in environments with S-shaped hodographs? Tornadoes cannot just form out of nothing. They need a supportive/nurturing environment, which includes sufficient buoyancy to accompany that shear, and basically an absence of something else to screw all of that up. Downdrafts, outflow, and cold pools can be excellent tornado disruptors, especially since they are sources of negative buoyancy and downward accelerations (both of which are toxic to tornado production). Since environments with S-shaped hodographs tend to favor messy storms, it's usually the behavior of the parent thunderstorm that restricts or eliminates the favorable environment for a tornado to form. Tornadoes can still form if the environment doesn't get too messed up, but it is simply more common for disruption to occur with these hodographs.
My hypothesis about how impactful S-shaped hodographs can be on supercells
In the 2016 Severe Local Storms Conference, Matt Parker presented some research on the impact of VB on supercells (https://ams.confex.com/ams/28SLS/webprogram/Paper300986.html). A cursory examination of his results surprised me, as he tested several hodographs that featured either VB, a kink, or some sort of S-shape (all examples of the reversal of hodograph curvature). This led to a broad conclusion that VB really doesn't matter when it comes to supercell behavior. This result seems at odds with my own personal observations, and I think many other chasers would agree that storms seem to struggle to get or stay organized in environments with S-shaped hodographs. The research Matt did looks legitimate, so I had to follow along more closely to see where the discrepancy arises. My hypothesis is that the height of the inflection point (where the hodograph curvature reverses) is critical in determining whether supercells will thrive in an S-shaped hodograph environment. Specifically, when the inflection point is higher, it is more likely that supercells will thrive. A general threshold seems to be about 3 km AGL. In the 9 hodographs he tested (below; shamelessly ripped from his recorded presentation), the inflection point is below 3 km in only one hodograph - "the fish hook" - and that is the only case in which a sustained supercell does not appear:


This is a bit subtle, but here is the explanation. If you're familiar with SHARPPY, then you know the hodograph color changes from red to green at the 3 km AGL mark. In the 7 hodographs above that have an inflection point, in only "the fish hook" hodograph does the inflection point occur in the red section. Even though it appears visually slight, it is there. And the results show that a storm struggled to survive in that environment. Surprisingly, he did not discuss the 0-3 km SRH values in these hodographs except for "the fish hook" which had 69 m2/s2 0-3 km SRH, a puny value if you want supercells. 0-3 km shear (not SRH) has been shown in some recent research to be a potentially skillful discriminator between weak and strong tornadoes, and it's not much of a stretch to consider the discriminatory nature of 0-3 km SRH to supercell and tornado production in general. Matt did mention at the end of his talk that it would be worth testing the sensitivity of these simulations to the height of the inflection point, but to my knowledge this research has yet to be conducted. I suspect whoever does it will find decreasing sustainability/organization in storms as the height of the curvature reversal decreases.
TL;DR
When assessing the impact of VB(V) on storm organization, the height at which the backing begins is probably pretty important, with increased potential for sustained supercells with increasing height. So don't despair just because you see VB in a sounding. You can still get relatively clean supercells and tornadoes with S-shaped hodographs. In fact, there was a little nugget towards the end of Matt's presentation suggesting that above a certain height, some degree of backing can actually be beneficial in that it can restrict left movers/splits, thus keeping the environment relatively undisturbed and allowing storms to rage for much longer.
Last edited: